分步傅立叶光纤光束传播

dannie

光束传播

自版本5起，RP Fiber Power新增了光纤内光束传播的仿真功能，不仅支持光功率传输模拟，还可处理复杂折射率分布下的全复振幅动态传播，涵盖激光增益、克尔效应等物理过程。以下将阐述其核心原理及实现方法。有关设置和使用模型的功能等详细信息，请关注后续。

一般假设

由于光束传播的仿真计算要求极高，因此它受到了一些限制：

• 所有涉及的波基本上都需沿一个方向（称为Z方向）传播。由于采用了近轴近似法，它们的发散角必须远低于1 rad。折射率不连续处可能产生的反向传播波（如背反射）无法被建模。
• 波仅在激光增益的情况下相互作用，例如通过增益饱和。
• 仅考虑一个极化方向，即采用标量（而非矢量）模型。
• 受内存限制，网格点的数量（详见下文）必须受到控制。然而，可以在不保存局部振幅的情况下执行子步骤，从而能够对非常大的网格进行建模。
• 对于极大的网格，计算时间可能相当漫长，例如在具有高数值孔径的长光纤的情况下。
• 光束传播仿真无法直接与激光和放大器模型、反向传播波以及超短脉冲传播相结合。但数据可以交换，例如，可以将光束传播仿真的光束分布作为光纤放大器模型的输入。
  

使用的算法

光束传播仿真有多种不同的算法。RP Fiber Power采用的是分步傅立叶算法。在该算法中，光场沿Z方向的传播过程如下：

• 首先，将场转换到空间傅立叶域，并在此域中应用考虑衍射效应的相位因子（假设一个平均折射率的波矢量）。
• 然后，将场转换回空间域，并在此域中应用考虑折射率不均匀性（如光纤纤芯折射率增加）的相位因子。
• 最后，在存在激光活性离子的情况下应用激光增益（或吸收），若光纤具有非线性，则还需应用非线性变化。所有这些步骤都在空间域中完成。
  

只要z步长足够小，该方法的精度就很高，因为实际上衍射和空间相位变化的影响在空间中是连续分布的。对于折射率对比度较小的光纤和其他波导，z步长可以相对较大，在许多情况下远大于波长。有关所需步长大小的更多详细信息将在下文阐述。

所使用的算法天然地暗示了周期性边界条件：当波到达数值网格的边缘时，可以在对面重新进入网格。然而，这种行为是可以改变的（详见下文）。

请注意，对于锐利的折射率跳跃（阶跃折射率分布），数值误差可能会增加。因此，将阶跃函数替换为提供稍微平滑折射率过渡（在几个数值网格点内）的高阶超高斯函数是有益的。这可能更符合实际情况，因为真正的光纤通常具有平滑的过渡。

光束传播装置（Beam Propagation Devices）

在RP Fiber Power中，光束传播是通过“光束传播装置”进行仿真的，这些装置与光纤模型保持分离，仅用于传输光功率。它们拥有自己的数值网格、光通道、光谱数据等。

一个脚本可以定义多个光束传播装置，例如用于不同版本的设备、串联使用的多个设备，或者用于具有不同分辨率的仿真以进行健全性检查。

每个装置都有自己的数字网格，场分布可以通过插值从一个装置转移到另一个装置（如有必要）。

数值网格

每个光束传播装置都有一个矩形类型的数值网格，它跨越X和Y方向的一些范围，这些范围都以坐标系的原点为中心。x范围从–xmax到+xmax，y范围从–ymax到+ymax。x和y的限值可以独立选择，步长尺寸取决于 和 ， 和 是整数且必须为2的幂。

此外，网格跨越一个特定的z范围，其中z=0对应于波导的开始位置（在这里注入初始场），并且波在正z方向以步长 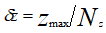传播到某个值zmax。

横向网格分辨率（即在x和y方向）必须足够高，以便对场的横向变化进行适当的采样。对于导模，这些变化的速度取决于光纤的数值孔径。例如，对于阶跃折射率光纤，相对于光纤轴（光纤内）的最大光束角大约为 (其中NA是光纤数值孔径)。那与最大横波矢量分量相对应 ，其中λ是真空中波长。由此我们可以得出结论，只要只关注导模（但如果包层模式不需要精确建模），大约为 的横向分辨率就足够了。这意味着，例如，单模光纤的导模通常可以采用比光束半径小几倍的横向步长尺寸进行采样，即使这比波长大得多。

网格的大小和边界处的行为：原则上，应使网格足够大，以覆盖所有可能出现不可忽略场振幅的区域。在实践中，将网格延伸到半径约为纤芯半径的两倍（甚至更小）通常就足够了。

但请注意，当场碰到网格的边界时，它会在另一侧重新进入网格。这种行为可能令人不安，因为它在物理上并不现实。可以通过引入人工损耗来抑制这种行为，人工损耗会快速而平稳地向网格边界增加。为了获得足够平滑的过渡，可能需要使网格更大一些。

还可以使网格边界在x和/或y方向上反射，或在x-y平面上定义任意形状的反射边界。

纵向分辨率必须非常精细，以确保在单个z步长内不会对场产生任何实质性影响（如衍射、折射率变化、损耗等）。换言之，上述效应都不应单独导致一个z步长中的场分布发生显著变化。例如，对于模式半径为5μm、波长为1μm的普通阶跃单模光纤，光纤中模式的瑞利长度约为120μm。当光束分布在一个瑞利长度内发生实质性变化时，步长尺寸应约为20μm或以下。对于模式较小和/或数值孔径较大的光纤，可能需要更小的步长尺寸。在某些情况下，步长尺寸可能大约是一个波长——这意味着为了将光传播到仅1mm的光纤上，就需要许多传播步长。

一般来说，例如当横向或纵向分辨率增加一倍时，建议测试仿真结果是否发生实质性变化。

原则上，光束传播不仅可以用于光纤和波导，还可以用于大型光学系统，如带透镜的自由空间光学系统。但是，如果涉及到较大的光束角度，横向分辨率需要很高，这将导致非常大的网格。此外，由于折射率对比度较大，可能需要非常精细的z步长。在这一领域，光束传播仿真可能存在一些实际的局限性。

光信道

每个光束传播装置可以包含多个“光通道”，每个通道具有不同的光波长。（即使波长很接近，也不考虑干涉和拍频效应）。对每个光通道都定义了折射率分布，折射率可以依赖于x和y，甚至z。对所有网格点计算用户定义的折射率函数。

使用的折射率分布可以通过光纤在x和y方向的曲率半径进行修改，这可能取决于z。例如，x方向的曲率被视为对所有与x坐标成比例的折射率分布的校正（注意：这种处理曲率的方法忽略了应力对玻璃的影响。对于二氧化硅光纤，已证明有效弯曲半径约是几何弯曲半径的1.28倍：应力效应部分补偿了几何效应。因此，应在软件中使用相应增加的弯曲半径）。

对每个光通道，还定义了作为初始场的二维复振幅分布，然后该分布会沿光纤传播。数值传播仅在通过某些函数请求特定z坐标下的振幅时自动进行。（因此，在进一步计算振幅之前，可以快速获得小z值的结果。）计算的振幅会被存储起来，以便稍后快速调用。此外，它们还可以在x-y平面内进行插值。我们可以生成各种各样的图表，这些图表可以依赖于数值网格中任何位置的振幅。

同一光束传播装置的不同光通道中的光场只有在存在激光放大或克尔非线性时才会相互作用（见下文）。

激光放大

光束传播装置的光纤可以包含激光活性离子。我们使用简化的增益模型，其中激光活性离子（如Er或Yb）仅具有一个亚稳态能级（较高的激光能级）。（允许准三能级行为，并且可以有多种类型的离子。）相关的光谱数据包括上态寿命以及作为波长函数的吸收和发射截面。

可以定义掺杂浓度的任意二维分布，但目前还不允许掺杂浓度对z的依赖性。

局部激光增益或吸收通常是根据稳态的局部光强度来计算的。或者，也可以进行动态仿真，其中用户定义某个时间间隔。在这种情况下，传播会模拟向稳态移动的上态粒子数的时间演变。

光通道之间会相互作用，因为它们可以影响激光活性离子的上态粒子数，从而影响所有通道的增益或吸收。

在某些情况下，人们可能只想对信号波进行光束传播，而不对泵浦波进行光束传播。泵浦的强度分布可以定义为用户指定的函数。这种方法的优点是提高了计算速度，并且可以模拟反向泵浦。当然，这种方法无法计算相互饱和效应；在确定泵浦的强度分布时，人们还不知道泵浦的强度是如何受到信号强度影响的。

克尔非线性

光束传播还可以考虑介质的克尔非线性。为此，用户可以定义材料的非线性指数，该指数可以是x和y的函数。例如，纤芯可能比包层更具非线性。

克尔非线性会导致一个光信道内的自相位调制(SPM)，也会导致同一光束传输设备的不同信道之间的交叉相位调制(XPM)。考虑到不同偏振方向的影响，用户可以降低交叉相位调制的强度。

受激拉曼散射

光束传播同样可以考虑受激拉曼散射(SRS)。这是由介质的延迟非线性响应引起的不同波长分量之间的相互作用。

适用于光束分布所有横向位置的仅仅是拉曼相互作用方程式（忽略所有其他相互作用）如下：

该方程用于更新光学振幅；除非也包括克尔非线性，否则不应用相位变化。

拉曼增益系数 既取决于一对相互作用波的光频差，也取决于横向坐标。