分享一下个人最近在学习的像差理论关于波像差部分:
几何像差直观易算,能够用数值来描述一点成像时的几何光线的密集程度,从而评估像质的优劣。但光线本身是一抽象的近似概念,用密集程度来评价,往往与实际不符,因此必须考虑像差的最佳校正方案,并根据光学系统的要求和使用状况给出合理像差。而这些像质评价问题常须基于光的波动本质才能解决。
几何光学中的光学相当于波阵面的法线,因此,物点发出的同心光束与球面波对应。如果光学系统是理想的,经过光学系统后会形成一个新的球面波,而实际上往往或多或少变了形不是理想球面波。实际波面和理想球面波的偏差就是波像差(wave aberration),即实际波面和理想波面之间的光程差。
波像差是各种几何像差的综合表现,加工、装配等带来的误差(比如倾斜、变形)也会在波像差当中体现出来。因此为改进设计、提高装配精度提供依据,将波像差表示成由离焦、倾斜和各种像差迭加而成的函数形式。在波面检测中,常常根据波面干涉图及其移动情况分解出波像差一般表达式中的各项,这种情况大多采用泽尼克圆多项式(Zernike polynomial)表示波像差,其中各项都有明确的物理意义,易于从中分离出各种像差。在出瞳上按极坐标归一化坐标 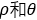 之后利用泽尼克圆多项式展开的波像差为:

以下是泽尼克多项式前九项: 若各项系数分别为Z0, Z1 ,……,Z8 ,则用泽尼克多项式前九项表示的波像差为: 上式中各项均有明确的物理意义,除常数项外, 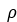 的一次项表示倾斜, 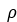 的二次项表示离焦和初级像散, 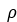 的三次项表示初级慧差, 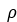 的四次项表示球差。高精度光学镜头也常对泽尼克多项式各项系数提出要求。 波像差和几何像差之间有着较为方便和直接的联系,因此,以最大波像差为评价依据的瑞利判据是一种方便而实用的相质评价方法,利用它可由波像差的允许值得到几何像差的容限。但它只是适用于评价望远镜和显微物镜等小像差系统(视场很小而孔径较大的体统,须校正好球差、色差和近轴慧差,使最大波像差不大于1/4波长,符合瑞利判据的要求) 当然,现代 光学设计已经从像差的优化转换为主要评价系统的综合像质,不必拘泥于几何像差的具体数值。但不代表只采用综合性评价指标就可以了,在采用波像差计算的传递函数时,需要对于畸变要特别注意。
光学设计是一项非常个性化的工作,同样的指标每个人都有设计出不同的光学系统,设计者需要有很好的像差理论功底。一方面对像差理论的应用极大影响设计进程和设计结果,对加工等也带来方便,另一方面是像投影光刻这样的极高精度光学系统甚至直接对波像差的Zernike多项式各项系数提出具体指标。
再提到软件使用时查看波前图,以Zemax软件提供的 Double Gauss28 degree field.zmx文件为例 该光学系统的波前图如下:
该图给出的pv值为0.9955个波长,rms为0.2592个波长,个人理解是给出设计pv和rms要求,达到设计要求即可,且优化采取波前优化算法才会考虑看波前图。
以上就是我个人对波像差的理解,欢迎各位朋友交流斧正,谢谢!
|  /1
/1 